CHERCHEUR DE CHOUETTE        

              LES SOLUTIONS DE DELPHINUS                       

      le PASS ou AUSWEIS est obscène  les psychopass sont des moutons    

 

 

La chasse "Sur la trace de la Chouette d'Or" est un jeu de sagacité, qui demande une ouverture d'esprit tournée sur la capacité de l'individu à disposer pleinement et en toute conscience d'un esprit critique et rationnel indépendant.

On ne peut se dire cartésien et astucieux dans un jeu de sagacité sans remettre en question ses solutions tout comme les dogmes imposés par une civilisation occidentale qui tend à uniformiser, contrôler et orienter nos modes de pensée par un politiquement correct, vers un Ministère de la Vérité, sans rejeter de facto le chant des Sirènes qui nous attirent vers l'échec et le chaos.

Ignorez les savants auto-philosophes proclamés qui ont tout compris des solutions de cette chasse, ignorez les grenouilles gonflées de vanité, les prétentieux et les inconscients, vous n'avez ni dieu ni maître, tout repose sur votre capacité à remettre en cause le communément admis  : soyez libertaires, créatifs, soyez intelligents !

“Le pire ennemi de la connaissance n’est pas l’ignorance, mais l’illusion de la connaissance” 

 Stephen Hawking

 

"La bêtise est infiniment plus fascinante que l'intelligence, infiniment plus profonde. L'intelligence a des limites, la bêtise n'en a pas. "

Claude Chabrol

 

à l'attention de la philosophe autoproclamée  Elizabeth Badinter qui semble ignorer la définition du mot génocide concernant la Palestine

Génocide : Crime contre l'humanité tendant à la destruction totale ou partielle d'un groupe national, ethnique, racial ou religieux ; sont qualifiés de génocide les atteintes volontaires à la vie, à l'intégrité physique ou psychique, la soumission à des conditions d'existence mettant en péril la vie du groupe, les entraves aux naissances et les transferts forcés d'enfants qui visent à un tel but.

 

HOLOCAUSTE des Palestiniens

Le président nicaraguayen Daniel Ortega a tenu des déclarations sévères contre le Premier ministre israélien Benjamin Netanyahu et le président ukrainien Vladimir Zelensky, les comparant au leader de l'Allemagne nazie Adolf Hitler. Ortega a qualifié Netanyahu de « nouvel Hitler » et Zelensky de « nazi » et de « fils d’Hitler », accusant le dirigeant ukrainien de tenter d’entraîner l’OTAN dans un conflit avec la Russie.

« Netanyahu se comporte comme un nouvel Hitler, poursuivant une politique agressive envers le peuple palestinien et les pays voisins. » - a déclaré Ortega lors de son discours.

Il a souligné que les actions d'Israël contre les Palestiniens lui rappellent les méthodes de l'Allemagne nazie pendant la Seconde Guerre mondiale.
 

il a parfaitement raison, et notre Prez n'a pas de couilles o pas de cerveau  pour le dire !

acquis indispensables :

la mesure dans le jeu est l'aulne qui possède 2 valeurs codées dans les énigmes (2 valeurs trouvées pour le moment, peut-être plus) : l'aulne de PARIS qui vaut 1,188 m depuis la 780 et depuis la 580 la nouvelle valeur de la mesure est l'aulne de LAVAL qui vaut 1,43 m ou plus exactement 1,432 m

sa confirmation 1,43 m provient aussi de l'énigme 600 qui possède 143 caractères et de la découverte de la ville de SCAER

sa précision est donnée par la 780 avec l'utilisation de pi = 22/7 soit 3,142 anagramme de 1,432 (22/7 est la valeur calculée par Pythagore, savant grec : rébus du visuel M GREC)

le décryptage de 2424... en code Morse donne CARIGNAN dans les Ardennes (traité des Pyrénées signé sur l'Île des Faisans)
 

la DCA droite connue avant est la droite MALO LES BAINS (DUNKERQUE) - ASCQ - CARIGNAN  voir le lien : La DCA

en effet :

- la distance SCAER - CARIGNAN est de 666 km soit 560606 x 1,188 m

- l'astuce sur l'utilisation de la mesure donne 253 km  voir le thème la Chose Importante (la CI) voir le lien : la Chose Importante

pour déterminer la DCA  nous convertissons les nombres en lettres, 560606 x 1,118 = 666 km et nous utilisons donc la Chose Importante découverte en 780

SIXCENTSOIXANTESIX = 253 en A1 soit 253 km et nous voyons que MALO LES BAINS est exactement à 253 km de CARIGNAN

or dans l'énigme 600, 253 c'était la valeur de la masse atomique de l'einsteinium de symbole Es et la date de naissance de  Clavius le 25 mars soit 25/3

nous avons confirmation de l'importance de l'einsteinium  en 600 qui sert immédiatement dans l'énigme suivante

grâce à cette astuce et par le fait que la ville d'ASCQ est l'anagramme de l'acronyme de SAQC (Spirale à Quatre Centres)  conformément au titre de l'énigme concernant le nom des notes, nous nous apercevons que la droite ASCQ - CARIGNAN se poursuit sur MALO LES BAINS située à une distance de 253 km de CARIGNAN.

emplacement de l'ancienne ville ASCQ sur la 989

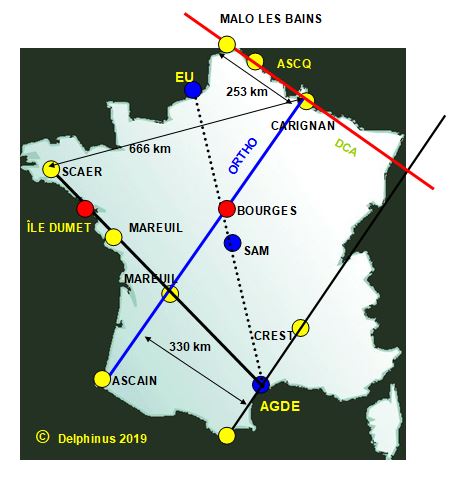
maintenant, ayant en poche l'orthogonale, nous cherchons un point situé à 803 km de CARIGNAN, en effet 560606 x 1,432 = 803 km

notons que sur ce cercle de 803km on passe sur DAX dont le blason

était à la fois une aide et une éventuelle  diversion : ACQS anagramme de SAQC

l'intersection du cercle et de l'orthogonale se trouve grâce à une recherche sur l'Atlas routier Michelin qui pointe la ville de MAGESCQ

la ville la plus proche de MAGESCQ est AZUR soit la couleur du ciel du visuel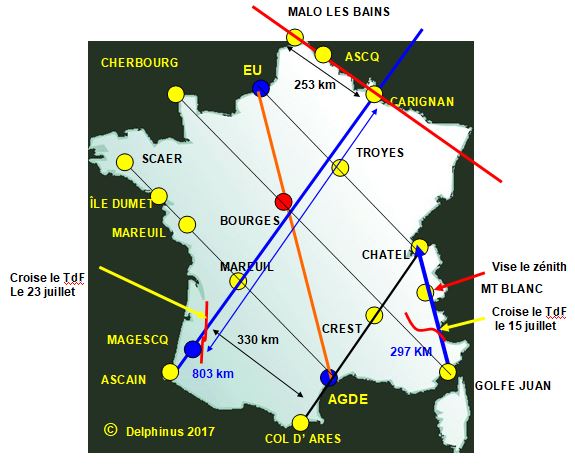

nota : sur ce schéma figure aussi la solution de l'énigme suivante la 420, ceci afin de voir que la DCA est confirmée dans l'énigme suivante par le fait que l'orthogonale est rigoureusement parallèle à la droite trouvée en 420, le résultat de la 420 valide l'étape précédente.

par ailleurs la portée musicale du visuel montre des lignes parallèles ce qui incite à penser que cela sera à exploiter en 500 ou 420

le nom de MAGESCQ procède du rapprochement de MEGA et SAQC, or SAQC est l'acronyme de Spirale A Quatre Centres (en rapport avec MAMEMIMOMU et l'utilisation et l'invention de la solmisation indiquée par le titre), nous avons donc bien utilisé le mot MEGA du texte

on peut dessiner une SAQC de plusieurs façons dont lévogyre ou dextrogyre :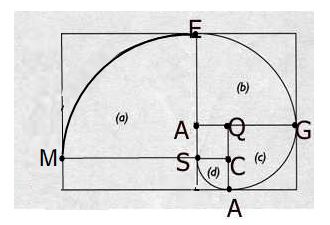

conclusion  : la SAQC se comprend avec un dessin que l'on fait après avoir trouvé le lieu à 560606 mesures de CARIGNAN en écrivant MEGASAQC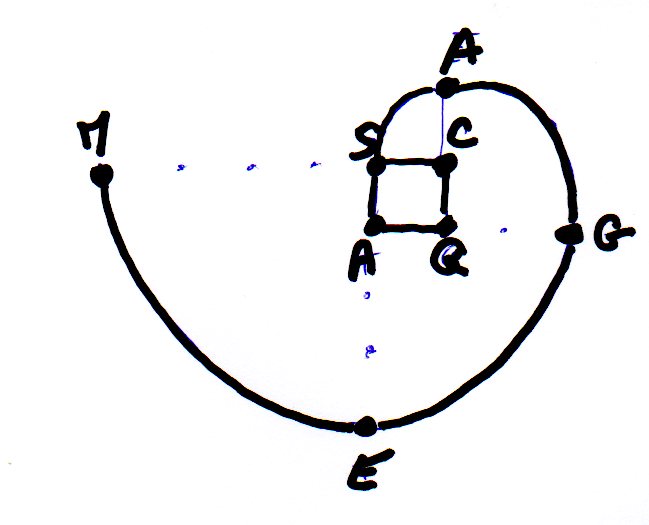

notons que les 8 points caractéristiques d'une SAQC où on peut écrire MEGA SAQC peuvent être confirmés ou avoir été un indice donné par les 8 graduations de l'équerre sur la règle du visuel.

sur le schéma ci-dessus nous avons bien en sens lévogyre MEGASAQC soit une lettre sur chacun des points constitutifs d'une véritable SAQC faisant un tour

ceci nous donne l'anagramme A MAGESCQ identique à la façon dont débute l'énigme par A CARIGNAN (ou A RONCEVAUX ou A CARUSBURC)

Wiki : Magescq est une commune française située dans le département des Landes en région Nouvelle-Aquitaine.
Localisation
Le nom Magescq viendrait du gascon mar signifiant la mer, et i ei signifiant y est, y fut. En effet, la mer a été présente à Magescq, il y a fort longtemps.
 

De gueules au pin maritime arraché de sinople, fûté d’argent, accosté de deux coquilles du même ; au chef losangé d’or et de gueules d’une tire

nous avons là sur le blason de MAGESCQ un pin, ce qui confirme le visuel de la 500 où figurent des "herbes" qui peuvent confirmer la forêt de pins des Landes, et notamment représenter des aiguilles de pins.

la confirmation :

la SAQC se trouve à 56060 aunes de CARIGNAN, soit 560606 x 1,432 m = 802787,792 m que nous arrondissons à 803 km sur la carte

une spirale de 803 km est construite à partir d'un carré de 802787,792 / 5 = 160557,5584 m

la diagonale du carré de base selon Pythagore fait :

racine de (160557,5584)² + (160557,5584)² = 227062 m soit 227 km soit encore la diagonale des visuels du livre 227 mm et le rapport avec la valeur de pi 22/7 utilisée en 780 pour obtenir 33 cm

  on comprend que la SAQC n'est pas à tracer car elle ne peut pas figurer en entier sur la carte 989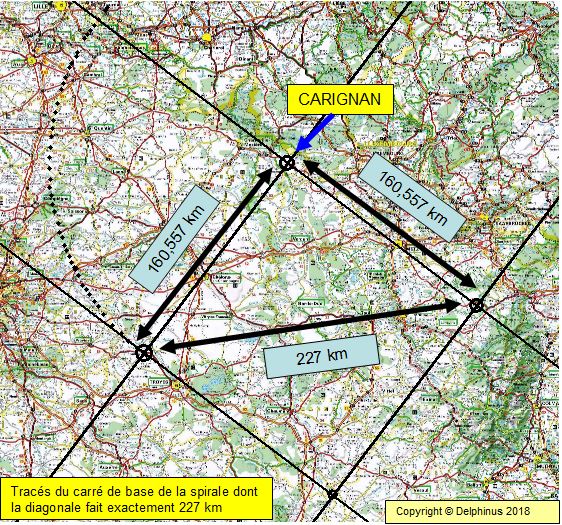

à ce stade là nous retrouvons 227 mm comme dimension de la diagonale du carré de base de la SAQC s'il avait fallu la tracer, et cette valeur de 227 mm est la dimension de la diagonale des visuels du livre.

[ Précédente ] [ Accueil ] [ Remonter ] [ Suivante ]

Pour me joindre chercheurdechouette@free.fr  pour toute question ou remarque concernant ce site Web.
Copyright © 2008-2020 Chercheur de Chouette
Dernière modification : 16 octobre 2024